Bachelor Quantum Physics notes (Norwegian/English)

• Return to the website

MAT1100: Calculus Sections

• Real numbers

• Induction proof

• Pascal’s triangle

• Complex numbers

• Euler’s identity

• Complex conjugates

• Complex roots

• The Fundamental Theorem of Algebra

• Functions

• Inverse functions

• Sequences

• Limits

• Epsilon–delta proof

• Vertical & horizontal asymptotes

• Intermediate Value Theorem

• Boundedness

• Extreme Value Theorem

• The derivative

• Derivative of inverse functions

• Mean Value Theorem

• Rolle’s Theorem

• Cauchy’s Mean Value Theorem

• Convex and concave

• All antiderivatives of a function differ by a constant

• Monotonicity Theorem

• Inflection point / Second derivative

• Practical use of derivatives

• L'hopital

• Oblique asymptote

• Riemann integrals

• Indefinte integrals

• The fundamental theorem of calculus

• Integration: Substitution

• Integration by parts

• Integration: partial fraction decomposition

• Improper integrals

• Arc length by integration

• Integration: volume about the x-axis

• Integration: volume about the y-axis

• First-order linear differential equation

• Modeling with differential equations

• Separable differential equations

• Recursive series

• Geometric series

• Convergence tests for series

• Taylorseries

• Taylor series remainder theorem

• Convergence of Taylor series

• Power series

• Finding the sum of series

• Arrow Left

Real Numbers

Real numbers are the foundation of calculus. It includes different number systems that are governed by theorems, and are often defined to be specific.

Lecture Notes

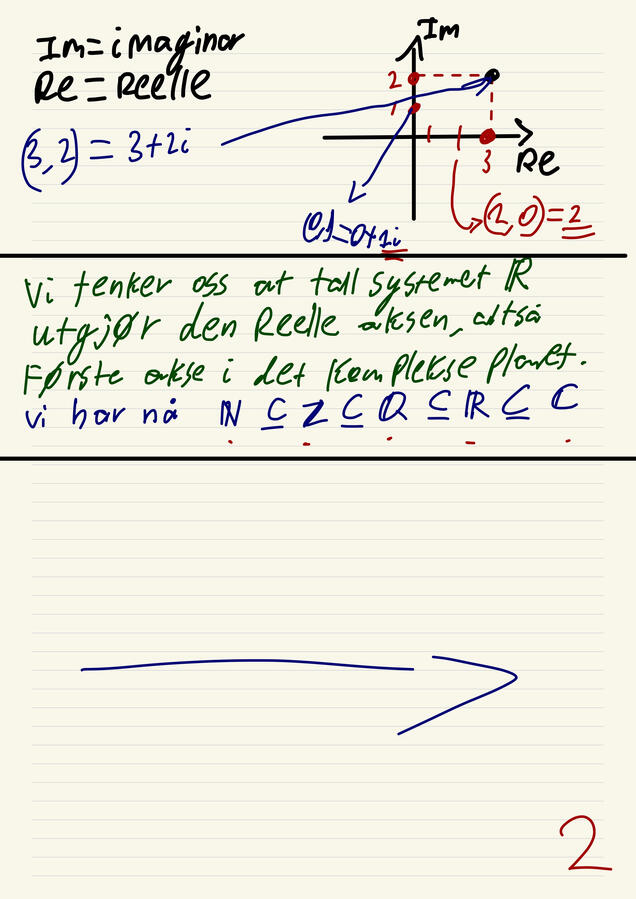
We notice a hierachy or number systems. Natural numbers (ℕ) are the lowest which means numbers like (1,2,3,4 etc). They dont account for negative numbers, for that we must include (ℤ) which entails integers. Now we have included numbers like (-1,-2,-3 etc). In order to include rational numbers such as (0.5, -0.3, 0.212 etc) we add another number system which are rational numbers (ℚ). Irrational numbers like pi or √2 are irrational and in a sense "infinite. So, we add real number (ℝ) which includes every real number! Later on we will discuss complex numbers (ℂ)Interval notation is how we apply symbols to indicate theorems/problems. for instance the symbol "(" means not includes. On page 3 at the top we can see an example entailing this. However, the symbol "[" entails that the superium IS included. Superium and inferium (SUP & INF) always include the last & first number, regardless if its in the number system we choose.

Examples

- Numbers between 2 and 5 (not included): (2, 5)- Numbers from 0 to 10 including both: [0, 10]- All numbers ≥ 4: [4, ∞)- All numbers < 3: (-∞, 3)

Key Properties / Theorems

• Arrow Left

Induction Proof

Induction is a powerful method for determining whether a recursive sequence is valid, consistent, and behaves as expected for all natural numbers. It allows you to verify that the sequence holds at its starting point and then prove that every subsequent step follows logically from the previous one. This makes induction one of the most reliable tools for establishing correctness in mathematical sequences and recursive definitions.

Lecture Notes

To use mathematical induction, we first start with a statement. This statement, P(1), must be shown to hold by proving that the left-hand side and the right-hand side of the formula are equal when (n = 1). Once the base case is verified, we assume that P(k) is true for some arbitrary natural number (k).If P(k) is true, then P(k+1) must also be true for the sequence to be valid. At this point, we get two different expressions: the known formula for P(k), and the formula we want to reach for P(k+1).The goal is to transform P(k) into P(k+1). We do this by adding the (k+1)-term to the left side of the equation and then adding the same term to the right side of P(k). Through algebraic manipulation, we show that the resulting expression matches the formula for P(k+1).Once this is done, the statement is proven by induction.

Examples

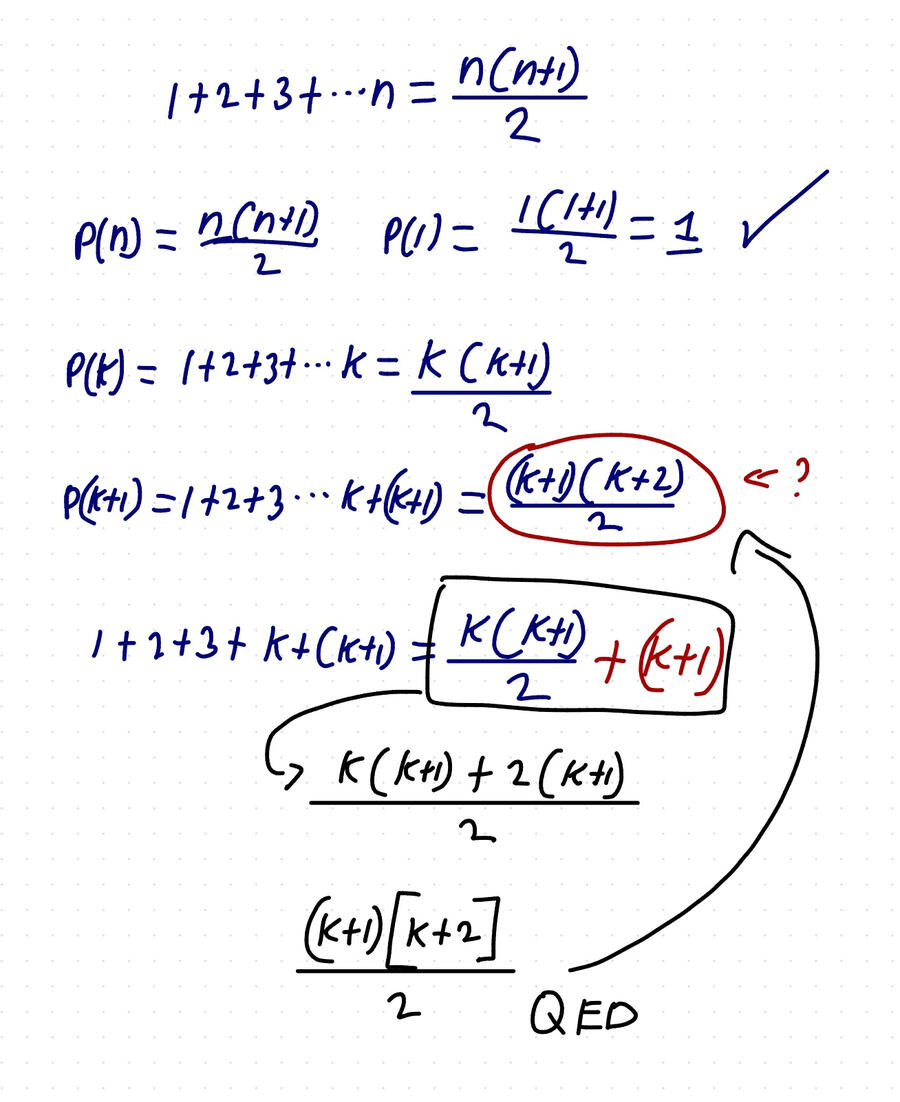
Comments

• Arrow Left

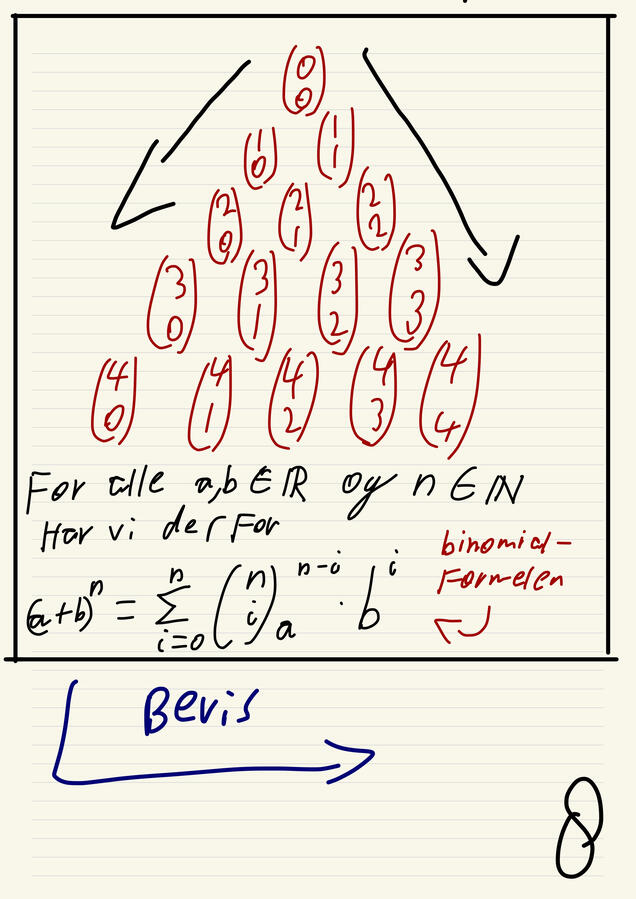
Pascal's Triangle

Pascal’s triangle is a core mathematical structure that appears throughout calculus and especially in probability. In my current course we focus on the essential idea rather than the advanced applications, which are covered in later probability semesters. At its heart, Pascal’s triangle forms one of the fundamental foundations of probability theory.

Lecture notes

Pascal’s triangle is the backbone of combinatorics. It’s the structure behind combinations, binomial coefficients, and countless counting problems. As you move into more advanced topics, you’ll start seeing it appear everywhere—from probability theory to algebraic identities and even certain areas of physics. Many of these deeper applications come in later courses, where the triangle becomes even more essential and its full power really shows.
The formula on the fourth page shows how it can be used to get the next or previous element in the triangle. This is the binomial formula!

Example

Problem 1: Out of 20 students, only 3 out of them gets chosen. What are the possible combinations?
we use the binomialformula to find the answer, we get then 1140 combinations.

Comments

• Arrow Left

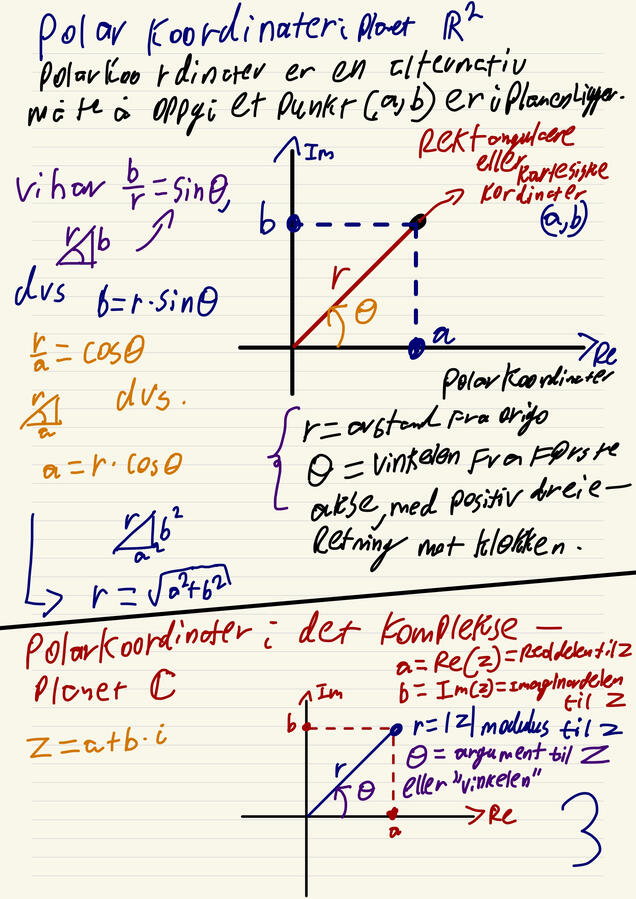
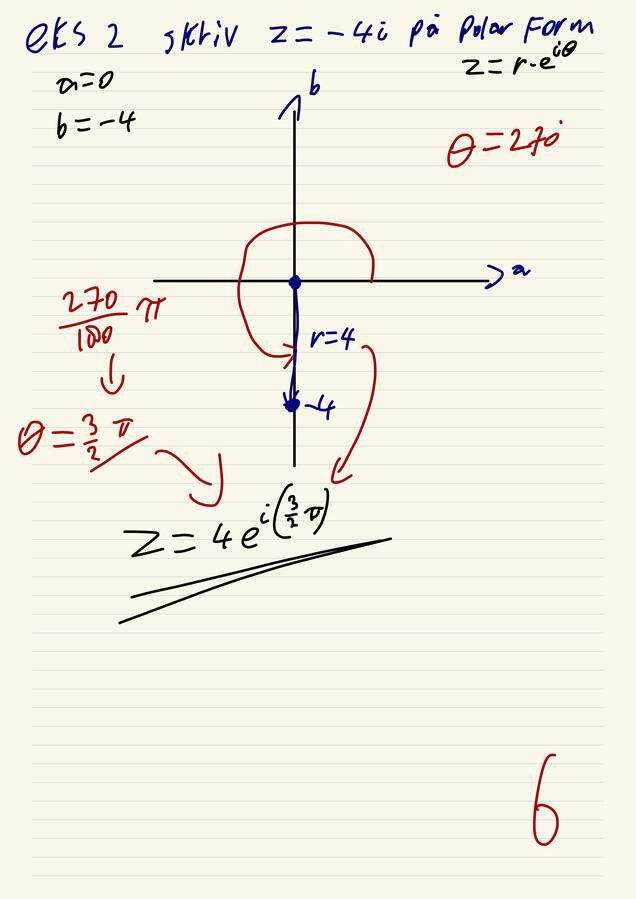
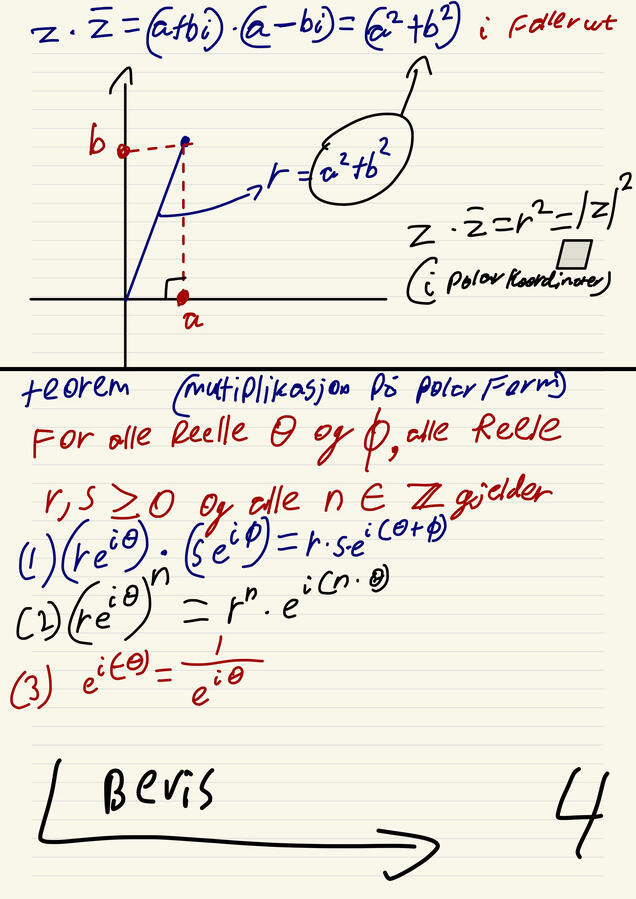
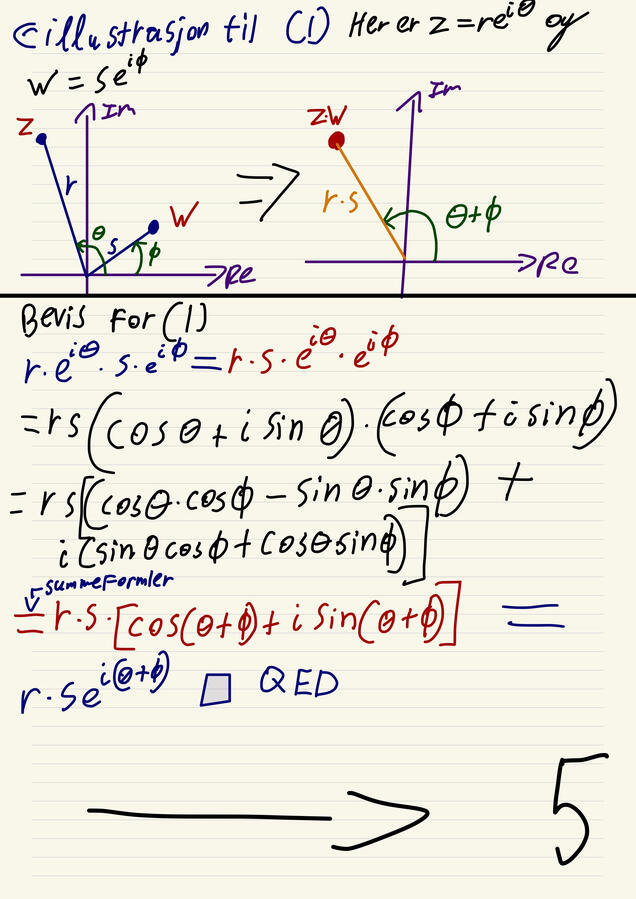
Complex numbers

For most of the time in history, √-1 has no solutions since, no number who are the same multiplied, make -1. So in math we invented a new symbol, i! the answer to √-1 is "i". this made a whole new field in calculus where we embark a new plane, other ways of making coordinates and more!

Lecture notes

• Arrow Left

FYS1100: Mechanics & modelling sections

• Fermiproblems

• kinematic equations

• Circular motion

• Separable Differential Equations

• Numerical solution of differential equations

• Work

• Kinetic and potential energy

• Conservation of energy

• Potential energy for variable forces (springs, gravitation)

• Oscillations

• Numerical differentiation and integration & rounding errors

• Thrust (driving force) & impulse

• Multi-particle systems

• Energy in rotational motion

• Torque

• Relativity theory: Simultaneity & The Lorentz transformation

• Length contraction and time dilation

• Relativity theory: Spacetime diagrams

• Relativistic momentum and energy

• Arrow Left

Fermiproblems

How do we make close approximations using only logic and simple math?
Through structured reasoning, we can build estimates that come surprisingly close to the real answer. This is the core of Fermi problems — breaking down an unknown into smaller, logical assumptions that we can justify. Enrico Fermi himself was famous for this skill. During the first atomic bomb test, he estimated the explosion’s strength by dropping small pieces of paper and observing how far the blast wave pushed them. No instruments. No data. Just logic, quick math, and a disciplined mind.

Examples

Problem 1: how fast does my hair grow every hour? let's assume i cut my hair once a month, when my hair becomes to get infront of my eyes. lets say from my eyebrows to my eyes the length is about 3-4 cm which is 0.00003–0.00004 km. 1 month equals to 30 days, which are 720 hours. now dividing the length to grow and the time we get 0.000000049 km/h.problem 2: how much PHYSICAL space does a 32 USB use? lets assume our USB is 4-6 cm in length, 1-2 cm in width and 0.5-1 cm in thickness. that makes the volume about 10 squared centimeters. 32 GB = 32 000 000 000 bytes. dividing the volume with bytes we get about 0.0000000003125 cm^3 / byte!

• Arrow Left

• Inflection point / Second derivative